(原創)Vertex Ranking Upbound on S(n,3)

A vertex ranking of a graph G is a mapping f fromV(G) to the set of all natural number such that for any path between two distinct vertices u and v withf(u)=f(v) there is a vertex w in the path f(w)>f(u).In this definition,we call the value f(v) the rank of thevertex v.

S(n, k) is a Sierpinski graph consisting of all n-tuples of integers 1, 2, . . . , k.

Vertex ranking of S(1,3) is 3.

Vertex ranking upbound of S(2,3) is 5?

Vertex ranking of S(2,3) is 5?

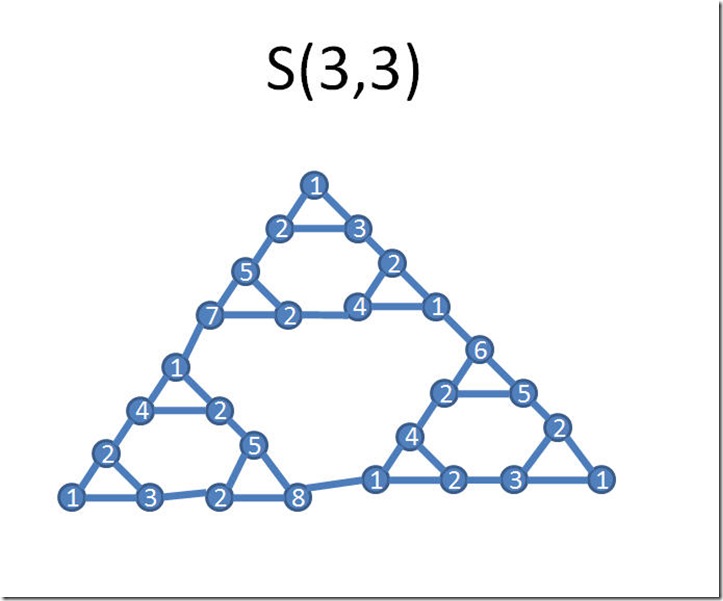
Vertex ranking upbound of S(3,3) is 8?

Vertex ranking of S(3,3) is 8?

Vertex ranking upbound of S(n,3) is 3n – 1 where n = 2,3,4,… ????

Vertex ranking of S(n,3) is ?????